Je me rappelle avoir pas mal galéré à comprendre le principe de la transformée en Z il y a quelques années. En relisant quelques articles sur le web, je viens de me rendre compte qu'en fait, ce n'est pas si dur que ça (que c'est même très simple dans le concept).
Dans cet article je vais donc essayer de vous décrire l'utilité de la transformée en Z.
La transformée en Z n'est rien d'autre qu'un cas particulier de la transformée de Laplace, bien connue de tout ingénieur. En réalité, il s'agit de la version discrète de la transformée de Laplace. Elle est donc utilisée dans le monde du numérique, notamment en traitement du signal (pour designer des filtres numériques par exemple) ou en automatique (pour asservir numériquement un système).
Au niveau mathématiques, on peut très facilement passer d'une transformée en Z à une transformée de Laplace. Il suffit de noter l'équivalence 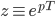 avec p, la variable complexe de Laplace et T la période d'échantillonnage du système (la transformée en Z travail dans les domaines discrets)
avec p, la variable complexe de Laplace et T la période d'échantillonnage du système (la transformée en Z travail dans les domaines discrets)
On se rend tout de suite compte que z représente donc un retard (En Laplace, 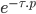 représente un retard de
représente un retard de 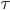 secondes).
secondes).
Du coup, 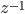 représente un retard de T secondes (soit un échantillon),
représente un retard de T secondes (soit un échantillon), 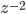 un retard de deux échantillons et ainsi de suite.
un retard de deux échantillons et ainsi de suite.
On voit donc que la transformée en Z manipule des échantillons avec plus ou moins de retard. C'est là tout l'intérêt de cette transformée, en lisant une équation, on peut donc facilement l'interpréter.
Pour plus d'information sur la transformée en Z, l'article de wikipédia est assez bien fait : http://fr.wikipedia.org/wiki/Transform%C3%A9e_en_Z

La transformée en Z, c'est le nom qu'on donné les gens pragmatiques (typiquement les ingénieurs et chercheurs en signaux discrets) aux séries formelles et séries génératrices des mathématiciens.
http://fr.wikipedia.org/wiki/S%C3%A9rie_formelle
http://fr.wikipedia.org/wiki/S%C3%A9rie_g%C3%A9n%C3%A9ratrice
C'est un très joli mariage entre un outil théorique et une application ultra utilisée. J'adore ça !
Par chance, on n'a pas besoin de l'un pour attaquer l'autre.