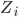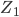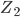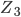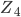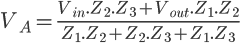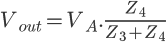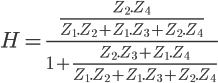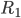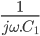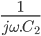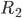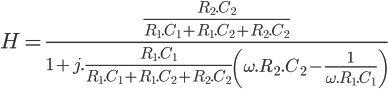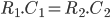Cet article fait parti du dossier Concevez vos PCB avec Kicad
 Dans un premier temps, il nous faut créer le schéma de principe du montage. Pour cela, vous pouvez cliquez sur le premier bouton de la partie droite de l’interface générale de Kicad. Ce bouton va vous permettre de lancer le logiciel «Eeschema».
Dans un premier temps, il nous faut créer le schéma de principe du montage. Pour cela, vous pouvez cliquez sur le premier bouton de la partie droite de l’interface générale de Kicad. Ce bouton va vous permettre de lancer le logiciel «Eeschema».
Le logiciel se lance et vous informe que le fichier «projet_tuto.sch» n’a pas été trouvé. Ce qui est normal vu que vous n’avez pas encore créé ce fichier !
Pour créer ce fichier, il vous suffit d’enregistrer une première fois le schéma (Avec le raccourci Ctrl+S par exemple). Un fichier à l'extension «.sch» est ainsi généré. Il contiendra votre schéma du montage.
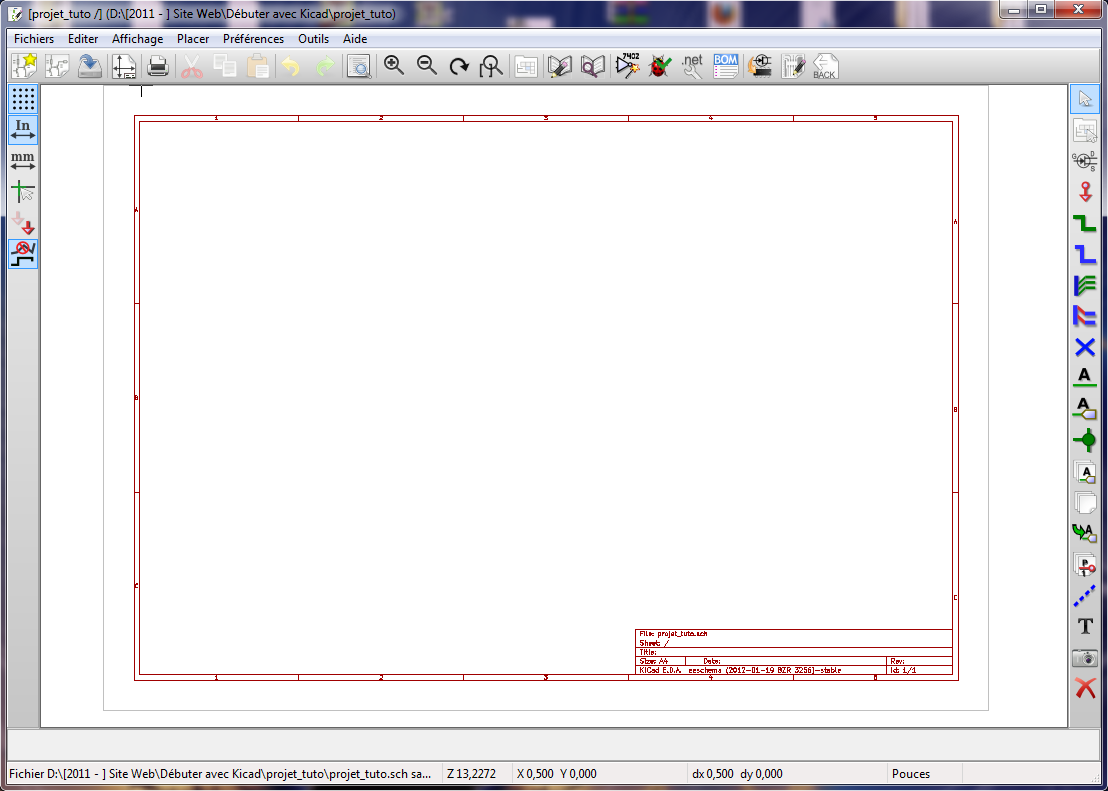
Vous arrivez maintenant sur une fenêtre vide.
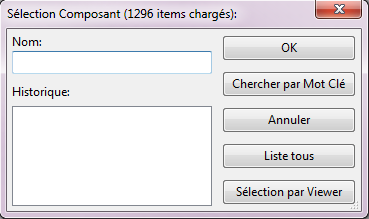
Nous allons commencer à placer des composants. Pour cela, cliquez sur le menu Placer=>Composants et cliquez sur la feuille de travail. Une fenêtre apparait alors et vous permet de choisir un composant.
Dans ma version de Kicad (du 19 janvier 2012), l’option «Recherche par Mot Clé» ne marche pas. Nous allons cliquer sur le bouton «Sélection par Viewer» afin de choisir notre composant.
La fenêtre de sélection est divisée en trois parties. La partie de gauche liste toutes les bibliothèques de composants intégrées à Kicad. Par exemple, la bibliothèque «conn» possèdera une liste de composants connecteurs, la bibliothèque «device» regroupera les composants communs tels que les résistances, condensateurs, transistors, etc.
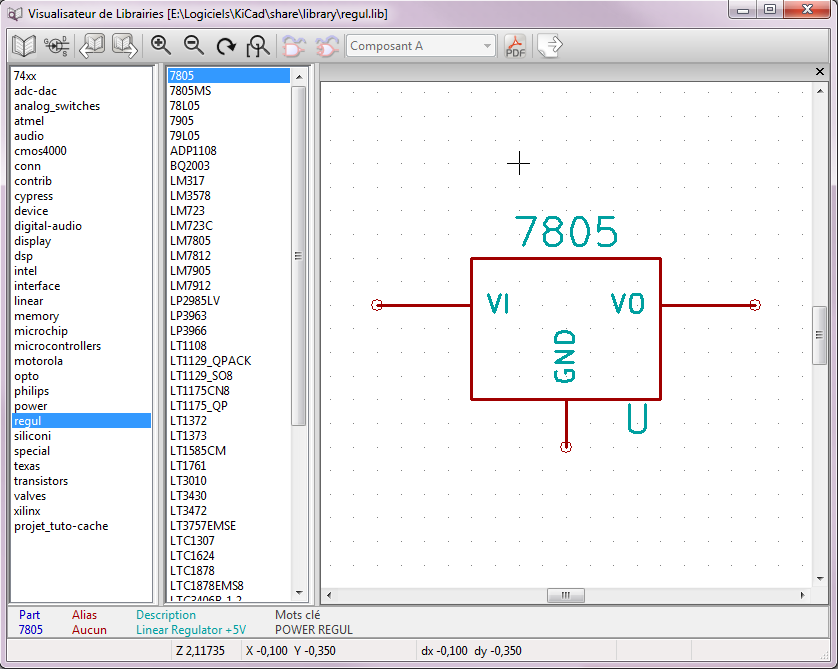
Ici, nous voulons créer un schéma d’une régulation 12V vers 5V afin d’alimenter un microcontroleur par exemple. Nous allons donc sélectionner la bibliothèque «regul».
La partie centrale du logiciel liste tous les composants présents dans la bibliothèque sélectionnée alors que la partie de droite nous permet de visualiser le composant sélectionné.
Ici, nous choisirons le régulateur 7805. Pour le sélectionner et le placer sur notre feuille, il suffit de cliquer sur le bouton «Placer le composant en schématique» en haut à droite de la fenêtre et de cliquer sur l’endroit de la feuille où vous souhaitez le placer.
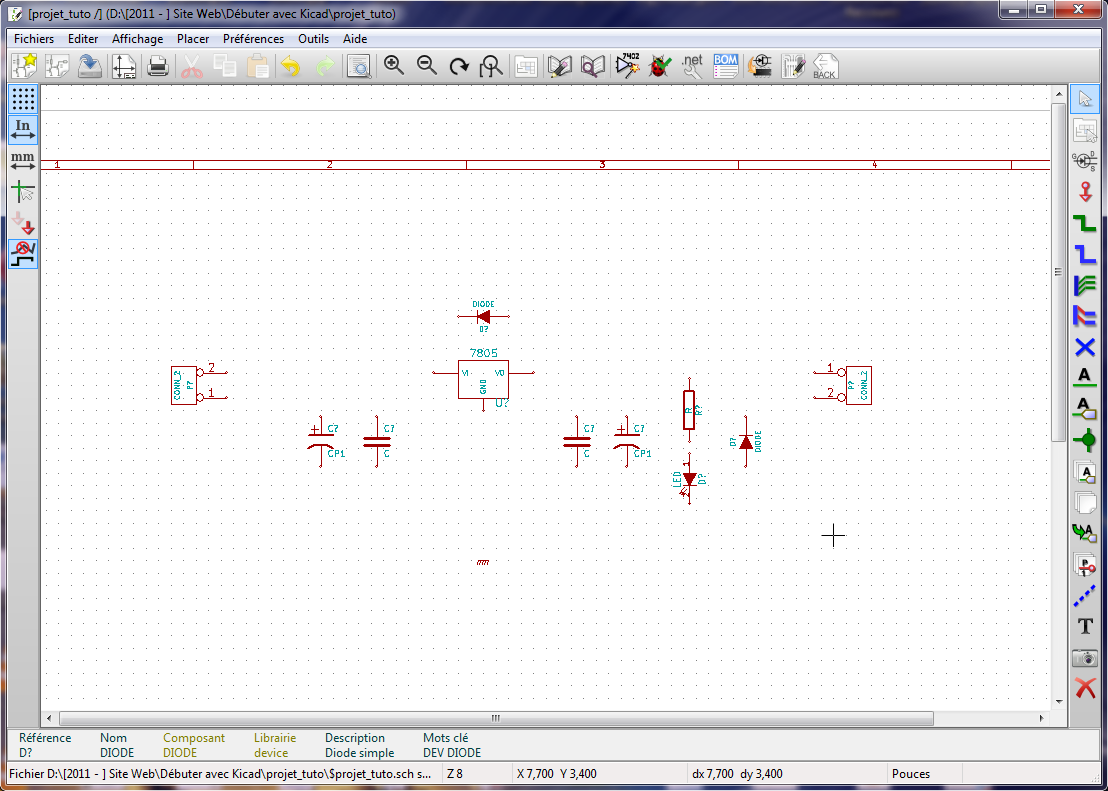
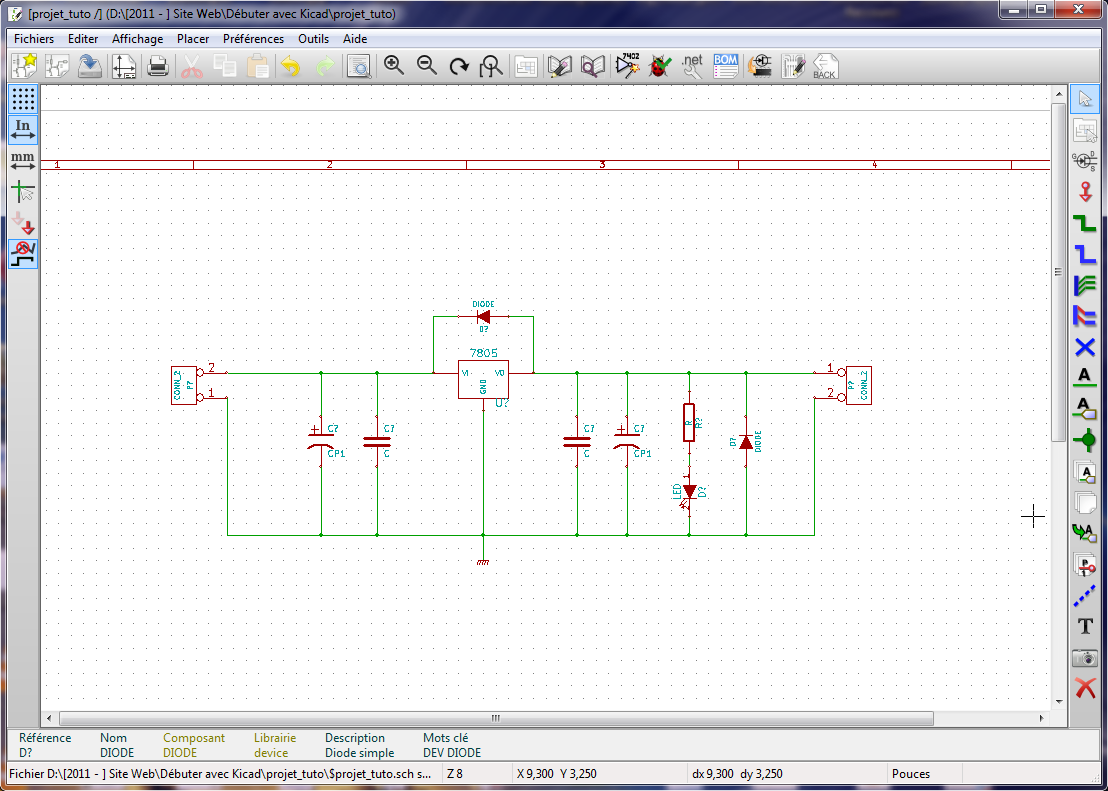
Faites la même chose avec les autres composants afin d’obtenir l’écran ci-dessous.
- Les condensateurs non polarisés se trouvent dans device/CP
- Les capa polarisés, dans device/CP1
- La résistance, dans device/R
- La LED, dans device/LED
- La diode dans device/DIODE
- Les connecteurs, dans conn/CONN_2
- La masse, dans power/GNDPWR
Pour déplacer le composant une fois celui-ci placé, mettez votre souris dessus et appuyez sur la touche M. Pour faire pivoter un composant, appuyez sur la touche R.
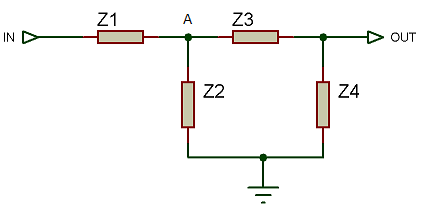
Maintenant, il ne nous reste plus qu’à placer les fils afin de relier les composants entre eux. Pour cela, cliquez sur le menu Placer=>Fil. Cliquez sur une patte d’un composant pour commencer à tracer un fil et cliquez sur la patte d’un autre composant ou sur un autre fil pour terminer l’opération. La touche Echap permet d’arrêter le traçage du fil en cours.
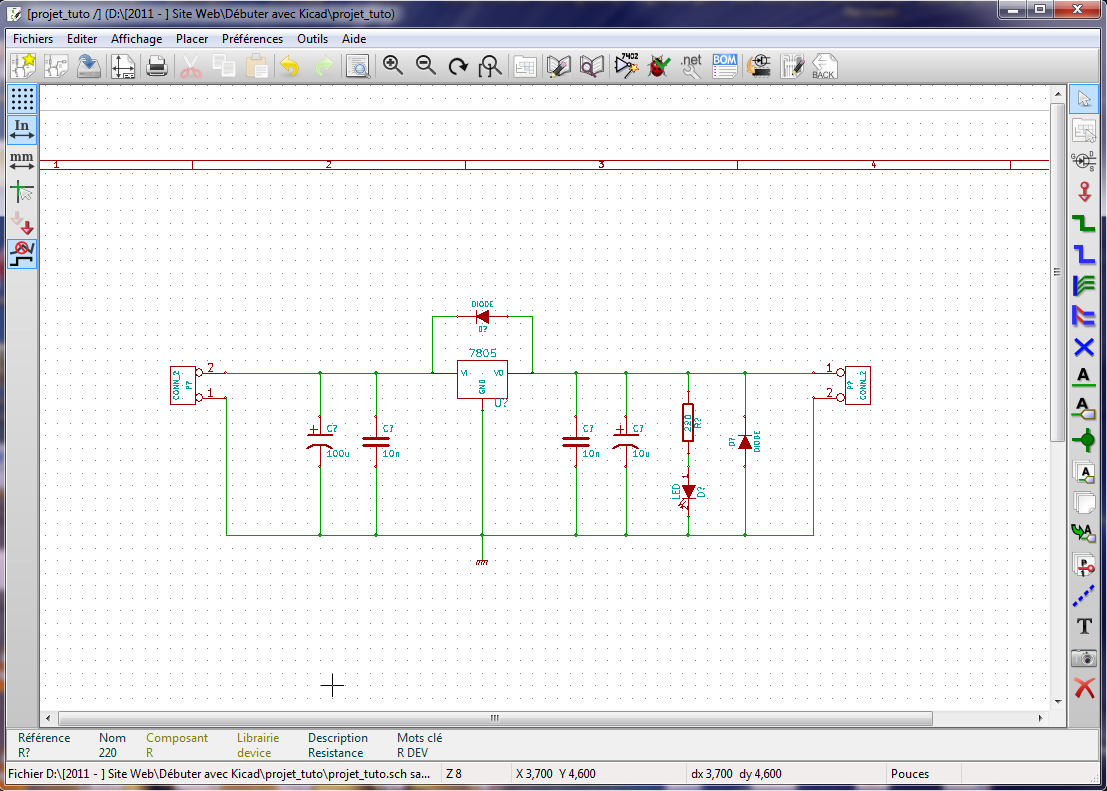
Votre schéma devrait ressembler à ça :
Il ne vous reste plus qu’à donner une valeur à chacun des composants en plaçant votre souris dessus, en appuyant sur la touche V et en renseignant la valeur. Cette étape est facultative, mais néanmoins conseillée.
Ce qui vous donne le schéma final suivant :
N’oubliez pas d’enregistrer le document si ce n’est pas déjà fait !
Arrivé à ce stade, afin de poursuivre la réalisation de votre circuit imprimé, il vous faut générer un fichier NetList (avec l’extension «.net»). Ce fichier vous permettra d’associer à chacun des composants de votre schéma, une empreinte.
![]() Pour générer ce fichier, il vous faut cliquer sur l’icône «Génération de la netlist» (cinquième icône en haut en partant de la droite).
Pour générer ce fichier, il vous faut cliquer sur l’icône «Génération de la netlist» (cinquième icône en haut en partant de la droite).
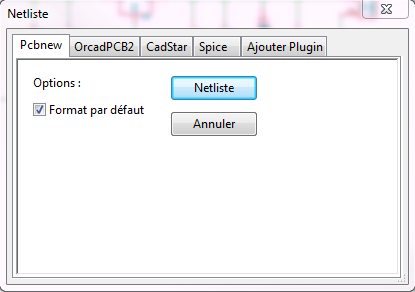
Dans le premier onglet (Pcbnew), cliquez sur le bouton NetListe.
Sauvegardez alors votre fichier à l’extension «.net» dans le dossier de votre projet. La première fois, le logiciel vous informera que certains composants ne sont pas numérotés. Dites que vous voulez les numéroter.
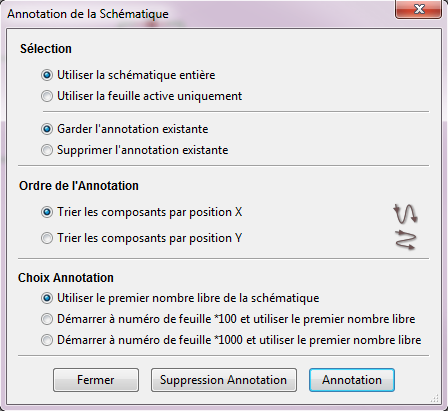
Vous arrivez sur une fenêtre avec des options. Laissez-les par défaut, ou modifiez-les à votre guise et cliquez sur le bouton «Annotation»
Les composants ont été numérotés automatiquement et la netlist a été généré. Fermez la fenêtre puis fermez le logiciel d’édition de schéma.
Vous êtes maintenant prêt à associer une empreinte à chacun des composants !