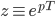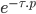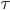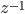Ferdinand Piette

Robocode : programmez votre IA !

Intelligence artificielle Pas de commentaires »

Mai 282011

Un petit article pour vous présenter une petite plateforme permettant de programmer une intelligence artificielle en java afin de contrôler un tank virtuel ! Vous pouvez se faire affronter entre eux des chars avec les IA que vous avez programmés ou téléchargés.

C'est un jeu de programmation libre développé par IBM. La plateforme est livrée avec des IA d'exemples ainsi que toute une bibliothèque fournissant déjà des fonctions de bases assez haut niveau vous permettant de vous déplacer, de récupérer des informations sur le terrain ou encore de faire feu.

Une fois votre IA programmé, vous pouvez affronter d'autre IA dans des tournois automatiques et ainsi voir l’efficacité de vos algorithmes.

Vous pouvez télécharger ce jeu sur le site de robocode : http://robocode.sourceforge.net/
Vous avez aussi accès à un wiki vous permettant de bien démarrer et de créer votre premier robot : http://robowiki.net/wiki/Robocode_Basics

Voici une petite vidéo montrant l'interface de combat ! Pour l'occasion, j'ai programmé une petite IA représenté par le robot Blacky1. J'ai implémenté un algorithme de déplacement par champs de potentiels modifié afin qu'il gravite autour du robot cible. J'ai aussi implémenté un algorithme de suivi de la cible avec le radar (le radar balayant à 45° autour de la cible). Enfin, l'algorithme de mise à feu prédit la trajectoire du robot cible de façon linéaire afin d'anticiper son mouvement. De plus, il calcule aussi la puissance du coup de feu en fonction de la vie de l'adversaire et de sa propre vie (tirer un coup coute de l'énergie !!)

J'ai donc fait affronter cette IA assez basique contre quelques exemples fournis avec le jeu. La vidéo est à la fin de l'article.

Ce jeu, très ludique, vous permettra de faire vos premiers pas dans le monde de l'IA, ou bien de tester des algorithmes assez complexes et de comparer leurs efficacités.
Amusez-vous bien ! 🙂

Téléchargez la vidéo en bonne qualité : http://www.ferdinandpiette.com/ressources/videos/robocode_demo.flv

Premier Topos : comment chercher un article sur le site

Accueil Pas de commentaires »

Mai 232011

Premier topos au bout de deux mois d’existence du site ! Le site est hébergé chez OVH et je n'ai pour le moment aucun problème. L'administration est efficace, le site charge rapidement (apparemment) et il n'y a pas encore eu de plantage. Pour le site en lui-même, j'ai installé un module WordPress qui permet de publier des articles. J'ai été agréablement surpris par la simplicité de ce CMS. Autant pour ajouter ou administrer le contenue que pour installer des plugins ou même bidouiller le code. Je le recommande à toute personne désirant créer son blog !

Dans ce billet, je vais juste vous présenter les différentes manières d'effectuer une recherche sur le site :

Les nouveaux articles

Sur la page d'accueil du site, j'ai mis en place un encart "Les 10 derniers articles" qui, comme son nom l'indique, recense les 10 derniers articles publiés sur le site, toutes catégories confondues (les articles de la catégorie "Accueil" n'y sont pas affichés, car vous pouvez les consulter directement sur la page d'accueil)

À la fin de cet encart, j'ai rajouté un lien Voir plus d'articles qui permet de visionner la liste complète des articles publiés sur le site, par ordre de publication.
De même, une fois sur la page listant tous les articles du site, vous avec la possibilité de visionner tous les articles, mais cette fois-ci triés par catégories, en cliquant sur le lien Voir tous les articles classés par catégories.

Les dossiers

Après avoir rédigé ma première petite dizaine d'article, je me suis rendu compte qu'il aurait été préférable de regrouper certains articles afin de faciliter la recherche. C'est pourquoi j'ai mis en place une page Les Dossiers (accessible dans le menu horizontale sous le titre du site) qui aura pour but de regrouper divers articles sur des thématiques précises.

Pour le moment, un premier dossier sur le filtre de Kalman regroupe les quatre articles complémentaires que j'ai écris à ce sujets. Par ailleurs, je viens de me lancer dans la construction d'une centrale inertielle. J'ai donc créé un dossier qui va répertorier tous les articles sur ce sujet !

Bien sûr, cette page Les Dossiers n'a pas pour vocation de recenser tous les articles, loin de là. Elle servira juste de page proposant des regroupements pertinents d'articles.

Les mots-clefs

J'ai associé plusieurs mots clefs à chacun des articles du site. Ces mots clefs essaye de caractériser l'article en question au mieux. Vous pouvez visionner ces mots clefs dans le menu latéral, à droite. Plus le mot clef est gros et plus il a été utilisé pour taguer des articles.
Si vous cliquez sur l'un des mots clefs, la liste des articles pour lesquels le mot clef a été associé apparaitra. Ces articles seront classés par date.

Les catégories

Toujours dans le menu latéral droit se trouve un widget recensant les catégories dans lesquelles les articles ont été placés. Pour le moment, j'associe un article à une et une seule catégorie. (Il se peut que je vienne à changer cette règle prochainement, mais je n'en éprouve pas l'utilité actuellement).
De même que pour les mots clefs, si vous cliquez sur une catégorie, vous verrez apparaitre tous les articles appartenant à la catégorie en question classés par date.

Les archives

Le widget "Archives" dans le menu latéral vous permettra de visionner un extrait des articles publiés le mois sélectionné.

La recherche

Et enfin, vous pouvez utiliser le module de recherche présent en haut à droite de la page, à côté du menu horizontal. Ce module permet de trouver tous les articles contenant les mots que vous avez saisis !

Voilà pour les moyens de trouver un article ! Vous n'avez plus qu'à choisir le moyen qui vous correspond le mieux ! 😀

Bonne lecture !

Centrale inertielle : Acte 1, Scène 1

Projets 9 commentaires »

Mai 212011

Depuis quelque temps, une idée me trotte dans la tête : construire une centrale inertielle capable d'être embarquée dans un petit drone quadrimoteur. Ça y est, je me lance enfin. Ce week-end, je viens de recevoir mes premiers capteurs qui vont me servir pour les premiers tests.

J'ai donc fais l'acquisition d'un accéléromètre 3 axes (ADXL335) permettant de détecter des accélérations allant de + à - 3g, ainsi que deux gyroscopes 2 axes (LPR530AL et LPY530AL) détectant des vitesses angulaires jusqu'à 300° par seconde. Ces trois composants ont des sorties analogiques et sont alimentés en 3.3V. Ils sont montés sur une platine Sparkfun permettant d'avoir facilement accès aux pins du composant (le composant lui-même étant en CMS).

Dans la foulée, j'en ai profité pour acheter une platine Arduino pour pouvoir rapatrier les données sur le PC sans me prendre la tête. Mais ne vous y trompez pas, je n'ai pas l'intention d'utiliser une Arduino pour le traitement des données ! C'est juste pour pouvoir faire des tests facilement. Le cahier des charges de la centrale n'est pas encore rédigé, mais je compte faire les traitements et la fusion des données sur un PIC33F de microchip ! (Le but de ce projet est d'avoir un module inertielle adaptable à tout projet et étant assez précis pour faire voler un robot)

La première étape de ce projet sera donc (outre la rédaction d'un mini cahier des charges pour savoir où je vais) de faire mumuse avec mes nouveaux composants : de caractériser leur bruit, d'identifier la dérive des gyroscopes et d'essayer de faire quelques traitements minimes sur les échantillons (filtrage et autre).

Dans un second temps seulement, j'essayerais de trouver une méthode de fusion efficace et performante. (Pour le moment, je pense me diriger vers un filtre de Kalman étendu. Je devrais probablement rajouter d'autre capteurs (comme des capteurs magnétiques ou autre boussoles par exemple)).

Mes nouveaux composants !

La suite au prochain épisode 😉

Le filtre de Kalman étendu : principe et exemple

Traitement du signal 19 commentaires »

Mai 212011

Lorsque vous souhaitez appliquer un filtre de Kalman pour estimer des paramètres d'un système, la première chose à faire est de modéliser votre problème. Il se trouve que dans certain cas, les équations qui permettent de modéliser le problème ne sont pas linéaires. De ce fait, le filtre de Kalman n'est plus applicable tel quel. Heureusement, il est tout de même possible d'estimer les paramètres du système à l'aide d'un filtre de Kalman dit étendu. Ce filtre permet en effet de linéariser localement le problème et donc d'appliquer les équations du filtre de Kalman classique.

Dans cet article, je vais donc vous décrire le fonctionnement d'un filtre de Kalman étendu, puis je reprendrais l'exemple de l'article http://www.ferdinandpiette.com/blog/2011/04/exemple-dutilisation-du-filtre-de-kalman/ afin d'utiliser un EKF (Extended Kalman Filter).

Pour pouvoir lire cet article, vous devez être familié avec le filtre de Kalman classique. Je vous conseille donc de lire la série de trois articles sur le filtre de Kalman que vous trouverez sur ce site : http://www.ferdinandpiette.com/blog/2011/04/premiers-articles-du-blog/

Algorithmes de planification de trajectoires : bref état de l'art

Robotique 2 commentaires »

Mai 082011

En robotique, on est souvent amené à devoir planifier des trajectoires pour permettre à un robot mobile de se déplacer d'un point initial à un point final. La planification de trajectoire est un sujet qui est souvent traité dans le domaine scientifique. Il existe donc pas mal d'algorithmes différents permettant de réaliser une telle tâche. Dans cet article, je présenterais certaines de ces méthodes en expliquant brièvement leur principe ainsi que leurs avantages et leurs inconvénients.

La transformée de Fourier discrète

Traitement du signal 2 commentaires »

Mai 042011

Voilà un petit article expliquant l'intérêt d'une transformée de Fourier. Je ferais une partie sur l'implémentation cette transformée et je parlerais des limites d'une telle méthode.

Le principe des filtres numériques

Traitement du signal 8 commentaires »

Avr 252011

La notion de filtre passe-bas, filtre passe-haut, coupe-bande ou passe-bande peut sembler familière aux électroniciens, en particulier si le signal à traiter est analogique. Un jeu de capacités, de résistances et éventuellement d'amplificateurs opérationnels suffit largement dans la majorité des cas. Le problème, c'est que tous ces beaux composants ne sont plus d'actualités lorsque l'on travaille avec des signaux numériques. A ce niveau, le concepteur d'un filtre numérique travaillera avec des microcontrôleurs ou des processeurs et manipulera un flux de nombre représentant le signal discrétisé.

Dans un monde utilisant de plus en plus le numérique, le filtrage numérique prend donc une place de plus en plus importante. On retrouve aujourd'hui des filtres numériques partout : dans les radios, les téléphones, les télévisions, les home cinémas, mais aussi en informatique, dans les logiciels de traitement audio, les lecteurs multimédias etc. Être capable de comprendre comment fonctionne de tels filtres est donc indispensable lorsque l'on touche au traitement du signal.

Nous allons donc voir dans cet article à quoi correspond concrètement les expressions mathématiques d'un filtre numérique (que l'on peut, par exemple, souvent trouver sur internet) et nous verrons comment implémenter de tels filtres dans un langage de programmation séquentiel. (Je vous fournirais ma bibliothèque codé en C)

La transformée en Z

Mathématiques 1 commentaire »

Avr 232011

Je me rappelle avoir pas mal galéré à comprendre le principe de la transformée en Z il y a quelques années. En relisant quelques articles sur le web, je viens de me rendre compte qu'en fait, ce n'est pas si dur que ça (que c'est même très simple dans le concept).
Dans cet article je vais donc essayer de vous décrire l'utilité de la transformée en Z.

La transformée en Z n'est rien d'autre qu'un cas particulier de la transformée de Laplace, bien connue de tout ingénieur. En réalité, il s'agit de la version discrète de la transformée de Laplace. Elle est donc utilisée dans le monde du numérique, notamment en traitement du signal (pour designer des filtres numériques par exemple) ou en automatique (pour asservir numériquement un système).

Au niveau mathématiques, on peut très facilement passer d'une transformée en Z à une transformée de Laplace. Il suffit de noter l'équivalence $z \equiv e^{pT}$ avec p, la variable complexe de Laplace et T la période d'échantillonnage du système (la transformée en Z travail dans les domaines discrets)

On se rend tout de suite compte que z représente donc un retard (En Laplace, $e^{-\tau.p}$ représente un retard de $\tau$ secondes).
Du coup, $z^{-1}$ représente un retard de T secondes (soit un échantillon), $z^{-2}$ un retard de deux échantillons et ainsi de suite.
On voit donc que la transformée en Z manipule des échantillons avec plus ou moins de retard. C'est là tout l'intérêt de cette transformée, en lisant une équation, on peut donc facilement l'interpréter.

Pour plus d'information sur la transformée en Z, l'article de wikipédia est assez bien fait : http://fr.wikipedia.org/wiki/Transform%C3%A9e_en_Z

Premiers articles du blog !!

Accueil 7 commentaires »

Avr 222011

Voila, pour inaugurer mon site internet, j'ai rédigé trois articles concernant le filtre de Kalman utilisé en traitement du signal.

Le premier article explique à quoi sert un tel filtre et quels en sont les limites. Le second est un article technique qui explique la signification des équations du filtre de Kalman (qui est une évolution de la méthode des moindres carrés) et enfin, le dernier article donne un exemple concret de l'utilisation d'un filtre de Kalman pour résoudre un problème de fusion de données multi-capteur.

Article 1 : Le filtre de Kalman : intérêts et limites
Article 2 : De l'estimateur optimal au filtre de Kalman
Article 3 : Exemple d'utilisation du filtre de Kalman

Si jamais vous avez un commentaire ou si vous détectez une boulette, n'hésitez pas à poster vos remarques à la suite de l'article en question !

Bonne lecture. 🙂
Ferdi

Exemple d'utilisation du filtre de Kalman

Traitement du signal 57 commentaires »

Avr 222011

Une centrale inertielle est un instrument de mesure de l'accélération et de la vitesse angulaire composé de trois accéléromètres et de trois gyroscopes. Estimer l'accélération et la vitesse angulaire pourrait sembler trivial dans la mesure où un accéléromètre fournit une mesure d'accélération et un gyroscope, une mesure de vitesse angulaire. Néanmoins, nous allons voir que dessous cette apparente facilité se cache des difficultés bien réelles.

Le but de cet article n'est pas de recréer une centrale inertielle, mais simplement d'essayer d'estimer l'angle d'inclinaison ainsi que la vitesse angulaire d'un objet selon un axe uniquement à l'aide d'un filtre de Kalman. Ce problème nous permettra non seulement de toucher du doigt la complexité de la mise en œuvre d'une centrale inertielle, mais aussi et surtout d'utiliser un filtre de Kalman afin de faire de la prédiction d'information et de la fusion de données multi-capteurs.

Page 3 sur 4 Articles plus récents 1 2 3 4 Articles plus anciens

Sciences et Techniques